Understanding Quantum Resistant Ledger

I been given task of researching any one of cryptocurrencies on the market. So after asking Grok Deep Search "give me list of most innovative latest cryptocurrencies". It gave me multiple cryptocurrencies that all look futuristic, but the one that got most of my attention was Quantum Resistant Leger (QRL), mostly because it has word "Quantum" in its name.

First I thought QRL is another one of those "talking but nothing inside" kind of crypto project. But after doing some digging. I found it was legit project with really cool ideas.

Whitepaper

Quick bits about QRL

QRL became available on exchanges around July 2018, shortly after its mainnet launch with the first block mined on July 26, 2018.

As of March 22, 2025, the current value of QRL is approximately $0.5120 USD.

How is this cryptocurrency unique?

It uses the eXtended Merkle Signature Scheme (XMSS), a hash-based digital signature scheme, to protect against potential quantum computing attacks that could compromise other blockchains like Bitcoin and Ethereum.

Bitcoin has a time between blocks of roughly 10 minutes. The QRL plans to safely use a block-time of 60 seconds with the help of newer ledger designs have improved upon this and benefit from a much shorter block-times (15 seconds) without the loss of security or miner centralization from high rates of orphan/stale block.

QRL uses a modified version of the Greedy Heaviest Observed Subtree protocol which allows stale/orphan blocks to be included in the blockchain and rewarded.

How can quantum computers break traditional digital signatures?

Traditional cryptographic systems, like those used in Bitcoin or Ethereum, rely on mathematical problems that are hard for classical computers to solve but easy to verify. Common problems are Factoring Large Numbers:

• This is the basis of RSA encryption. RSA uses a public key (made from the product of two large prime numbers) and a private key (derived from those primes).
• Example, if I give you the number 15, you can factor it into 3 × 5 easily, but if the number is hundreds of digits long, it takes a classical computer billions of years.
• Problem: Quantum computers can solve this efficiently using Shor’s algorithm, which can factor large numbers exponentially faster than classical computers.

Quantum computers use principles of quantum mechanics (like superposition and entanglement) to perform certain calculations much faster than classical computers. Specifically:

• Shor’s Algorithm:
  • Developed by Peter Shor in 1994, this quantum algorithm can factor large numbers and solve the discrete logarithm problem exponentially faster than classical algorithms.
  • For example, factoring a 2048-bit RSA key might take a classical computer billions of years, but a sufficiently powerful quantum computer could do it in hours or days.
  • This means that RSA and ECDSA (used in most blockchains) would become insecure once large-scale quantum computers are available.

Quantum Computers vs Traditional Computers.

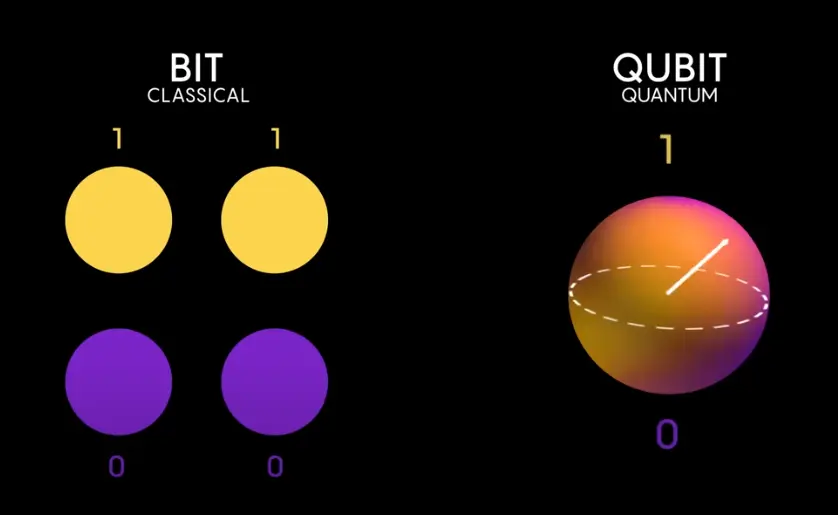
Traditional computers (like your laptop or smartphone) operate using classical bits:

• A bit is the smallest unit of information and can be either a 0 or a 1.
• These bits are processed using logic gates (like AND, OR, NOT) to perform calculations, following a step-by-step process (sequential or parallel in multi-core systems).
• For example, to solve a problem, a traditional computer might try every possible solution one by one (brute force) or use an optimized algorithm to reduce the number of steps.

Quantum computers use quantum bits, or qubits, which behave very differently from classical bits due to the principles of quantum mechanics:

1. Superposition:
   • A classical bit is either 0 or 1. A qubit can be in a state of 0, 1, or a superposition of both 0 and 1 at the same time.
   • This means a qubit can represent multiple states simultaneously. For example, 2 qubits can represent 4 states at once (00, 01, 10, 11), 3 qubits can represent 8 states, and (n) qubits can represent $2^n$ states.
   • This allows a quantum computer to process an exponentially large number of possibilities in parallel.
   • 
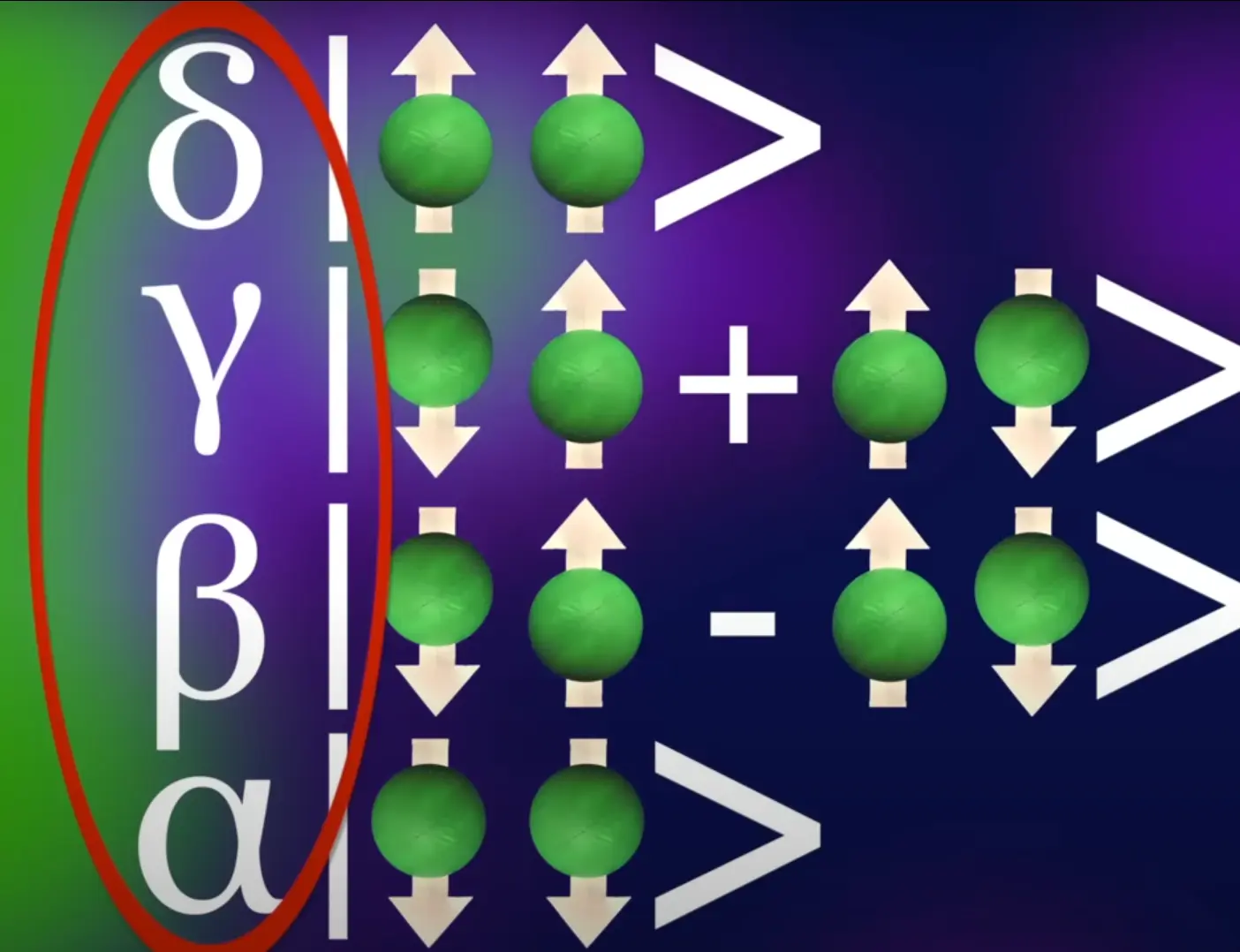
2. Entanglement:
   • Qubits can be entangled, meaning the state of one qubit is directly linked to the state of another, even if they’re far apart.
   • If you measure one qubit, the other’s state is instantly determined, no matter the distance.

More information

"So you should not think of a quantum computer as something where every operation is faster. In fact, every operation is probably going to be slower than in the computer you have at your desk.

But it is a computer where the number of operations required to arrive at the result is exponentially small.

So the improvement is not in the speed of the individual operation. It is in the total number of operations you need to arrive at the result."

What is eXtended Merkle Signature Scheme?

XMSS is a stateful, hash-based signature scheme that builds on W-OTS+ by combining it with a Merkle tree structure. It has the smallest signatures out of such schemes and comes with a multi-tree variant that solves the problem of slow key generation.
In particular, it is not required that the cryptographic hash function is collision-resistant for the security of XMSS.

Why is XMSS Quantum-Resistant?

XMSS relies on hash functions (like SHA-256), not on math problems like factoring large numbers (which quantum computers can solve easily). Hash functions are believed to be secure against quantum attacks, even with algorithms like Grover’s algorithm, which only gives a modest speedup to brute-force attacks.

XMSS for 5 years old.

• You have a big book of 1 million one-time-use stamps (one-time key pairs).
• You pick an unused stamp, sign the letter with it, and include a map (Merkle path) showing how that stamp connects to your official seal (the Merkle root, your main public key).
• The recipient checks the stamp’s signature, follows the map to confirm it matches your official seal, and knows the letter is really from you.
• You tear out that stamp from your book so you don’t use it again by mistake.

Why XMSS used in QRL?

Traditional digital signatures (like those used in Bitcoin, based on elliptic curve cryptography or ECDSA) can be broken by quantum computers using algorithms like Shor’s algorithm. XMSS is designed to be secure even against quantum computers, which is why QRL uses it to future-proof its blockchain.

Cons of XMSS

• Larger signatures: Makes transactions bigger (3KB in QRL), increasing storage and bandwidth needs.
• Stateful: You must track which keys you’ve used, which can be tricky for users (QRL’s wallet software helps manage this).
• Limited signatures: Each XMSS key can only sign a finite number of transactions after which you need a new key.

Key Features of XMSS in QRL

1. Large Signatures: Each XMSS signature is around 3KB, much larger than ECDSA signatures (around 70 bytes), due to the one-time signature, OTS public key, and Merkle path.
2. Single-Use Addresses: Because XMSS is stateful, QRL addresses can only be used once safely. After sending a transaction, you shouldn’t reuse the address.
3. Finite Signatures: An XMSS key can only sign a limited number of messages. After that, you need a new XMSS key.
4. Security: XMSS is approved by standards like NIST and is provably secure as long as the underlying hash function (e.g., SHA-256) remains secure.

What is Greedy Heaviest Observed Subtree?

The Greedy Heaviest Observed Subtree (GHOST) protocol is a consensus mechanism designed to improve the scalability, security, and efficiency of blockchain networks, particularly those using Proof-of-Work (PoW).

Background: In Bitcoin, the blockchain follows the "longest chain" rule: the valid chain is the one with the most blocks, representing the greatest cumulative computational work (assuming equal difficulty per block). However, this approach has a limitation—when blocks are created quickly (e.g., due to short block times), network latency can cause multiple miners to produce valid blocks at nearly the same time. Only one of these blocks gets added to the main chain, while the others become "stale" or "orphan" blocks, discarded and unrewarded. This wastes computational effort and can reduce security, as the discarded work doesn’t contribute to the chain’s defense against attacks.

How GHOST Works?

GHOST modifies this by shifting the focus from the "longest" chain to the "heaviest" subtree. Here’s the core idea:

1. Incorporating Stale Blocks: Instead of ignoring stale/orphan blocks (valid blocks that don’t make it into the main chain), GHOST includes them in the decision-making process.
2. Heaviest Subtree Rule: When a fork occurs (multiple valid chains exist), GHOST evaluates all branches, including the main chain and its offshoots (subtrees). It calculates the total weight of each subtree by summing the computational work (e.g., difficulty) of the main chain blocks and the valid stale blocks referencing them. The "heaviest" subtree—i.e., the one with the most accumulated work—becomes the canonical(official) chain.
3. Example:
   • Imagine a blockchain forks into two branches due to two miners solving blocks simultaneously:
     • Chain A: 5 blocks (total difficulty = 50).
     • Chain B: 4 blocks (total difficulty = 40), but it has 2 stale blocks (total difficulty = 20) referencing its earlier blocks.
   • Under the longest chain rule, Chain A wins (5 blocks > 4 blocks). But with GHOST:
     • Chain A’s weight = 50 (no stale blocks).
     • Chain B’s weight = 40 (main chain) + 20 (stale blocks) = 60. Chain B becomes the canonical chain because it’s "heavier," even though it’s shorter.

Note: stale blocks/orphan blocks, are valid blocks that are mined but do not become part of the main blockchain.